
Individual and Group Math lessons.
I love math and I love teaching math! I believe that all students can succeed in math. I see all types of learners including those with learning differences such as auditory processing, language processing, memory, and attention issues as well as gifted learners who thrive on math complexity and want more challenge. I receive referrals from schools or neurologists for those in need of either extra math support or enrichment. Often, parents want their child performing at global math standards, so they enroll their child in lessons to supplement their school math program.
The Singapore program is compatible with both American and international school math programs. With its emphasis on a strong math foundation and learning in a sequential manner, layer upon layer, and high-level problem solving, students with Singapore Math experience transition easily into any middle school or high school math program.

I teach one-hour individual math lessons for students in grades 1-8 and 45-minute lessons for kindergarten age students. The lessons are taught at a library, a location convenient for you or at my home classroom studio. All lessons are in-person. Lessons are offered after school, weekends, during school breaks as well as during the school day if pull out is available. If parents would like students to be grouped together, I can accommodate if the grouping is homogeneous in terms of the scope of work to be taught and the pacing of the lessons.
Lessons are individualized based on
an initial and ongoing assessment.
Step 1
Step 1
An initial assessment is 45 minutes to one hour and determines the recommended scope of work and frequency of the lessons. Depending on the grade level of the student, how many gaps in the foundation to fill, and the child’s current ability to see patterns and use strategies, lessons may be once a week or twice a week. The assessment is intended to be low stress and an opportunity for your child and I to learn. As I assess, I teach so that I can start to understand how this student learns and so that the student is comfortable with how I teach. It is not graded but shared with the child and parent so that student, parent, and teacher can agree on shared goals. Your child will receive individualized lesson plans to meet these goals. Once our specific goals have been met and the foundational gaps have been filled, your child will no longer need lessons. It’s not endless tutoring. The lessons are designed to be efficient in targeting gaps and missing connections so that your child’s trajectory can be changed to one of success in math.
Step 2
Step 2
During the lesson, students enjoy working problems on wipe off dry erase boards. Each student is given a binder for homework and notes. The expectation for homework is about 20 minutes daily but may be increased or decreased based on developmental needs or the gap being filled. Parents are often pleasantly surprised that their child does the homework independently and without complaining. That’s because the homework is meaningful work at the child’s level and is building confidence. Math is making sense to them. Often, I will send short videos from the lesson so that students can practice at home just the way they practiced in the lesson. The videos also show the parents how their child should be practicing. Students do not do homework in silence. They are talking out loud to improve their thinking and metacognition.
Step 3
Step 3
Children are asked to make corrections to homework and tests. Corrections are important in teaching children to identify their errors and analyze what kind of errors are being made. Students are periodically given topical tests to ensure mastery. The goal in math is accuracy. Just the right amount of homework will be given to attain mastery. Quality of homework is emphasized over quantity. Students are taught good math work habits such as using a proper workspace, how to label for clarity, being neat and using pencil only. They are also taught effective test taking skills.
Your child will be provided with
Singapore math tools and curricula.
I teach my students with Singapore math curricula including assessments. I have an extensive library of Singapore math resources so I will be able to customize your child’s math program with resources that match your child’s learning abilities and needs. Your child will be provided with authentic Singapore math textbooks and workbooks. Additionally, I use a Math Fact Fluency program that I created for the purpose of catching students up as quickly as possible in math facts. The Math Fact Fluency program uses the Singapore methodology, is results based and works for all learning profiles.
I have a large collection of manipulatives available for my students to use as tools to help them think, reason, and solve problems. Children enjoy using manipulatives and stay engaged in the lesson. An important part of learning is choosing the appropriate tool for a given problem or situation. Students build confidence with manipulatives and other tools that provide a way to test and confirm their reasoning and make abstract ideas concrete and understandable.



Your child will be provided with
a Color Thinking Chart.
Your child will be taught to solve problems by using a tool that I developed called a Color Thinking Chart. This tool has been used by many students in many schools and has proven results. It was developed to help train your child’s brain to think both systematically, by sustaining focus through the problem, and creatively by using different strategies to solve the problem at hand. This chart turns mathematician George Polya’s four-stage thinking process (understand the problem, devise a plan, execute the plan, and look back and check) into a child friendly, color-coded format.
Yellow:
go slowly and read carefully
Red:
red light stop until you can clearly see the problem
Green:
go and choose your strategies
Blue:
ready to solve
Purple:
the metacognitive process of checking your work until both your steps and answer are confident

Your child will have this tool available during the lessons, homework, and tests. Children like the Color Thinking Chart so much that they’ve even taken it into their school classrooms to use and demonstrated it for other students to use.
This flowchart guides students through the problem-solving process. If a student likes to jump right to blue thinking without reading or understanding the directions and the problem, they’ll be redirected to yellow thinking and red thinking. If a student says he or she is finished after blue thinking, the student will be directed to purple thinking to check his or her work. If the child gets to blue thinking and the strategy fails, the child is directed back to green thinking to find the right strategy. This chart is constructed as a flip chart so that the child can lift the flaps and write inside them. For example, he or she may write notes inside the flaps such as strategies inside the green thinking flap.
Lessons are inquiry based and focused
on teaching critical thinking skills.
Asking questions and letting students discover the rules develops critical parts of the brain. True to the Singapore Math approach, each lesson is presented concretely and pictorially before abstract math language is used, contributing to the development of visualization in the occipital lobe of the brain and concept formation in the brain’s frontal lobe.

Metacognition, the mental function that manages what we do, is developed by asking students questions such as, “How do you know this is a dividing story?”, “Are you confident in your answer?’, and “How do you know your answer is correct?”. Questions that give students the opportunity to think about their thinking strengthen metacognition in the brain’s frontal lobe. As students internalize the questioning process, they learn to sort through confusion and achieve clarity of thought. In doing so, they’re developing abstract reasoning through the monitoring of their own thinking.
Metacognition and step-by-step problem solving are explicitly taught using the Color Thinking Chart. Through the purple color on the thinking chart, students are taught that they’re not through with a problem until they’re sure of their answer and their steps. Students learn to check their work by being taught to justify their answers orally and on paper. Students are taught to talk out loud to improve their metacognition and mental flexibility in problem solving developing in the brain’s frontal lobe. Math is not done in silence.
Math facts and procedures are committed to memory but only after the students see and understand the patterns and where the rules come from. Patterning is a mathematical competency that allows children to see trends and identify relationships among variables. After identifying the patterns, it’s imperative that students attain automatic recall of math facts (i.e., all facts are automatic like 1 + 1 = 2 with no thinking required). Having automatic recall of math facts frees up the brain for more complex problem solving. The same is true for long multiplication and long division procedures. Students should be able to calculate efficiently so their brain can focus on the harder process skills necessary for problem solving.
Although calculation and memory are important, the emphasis is on developing the higher-level thinking parts of the brain. That is, helping students develop visualization, critical thinking skills and the ability to effectively monitor and regulate their thinking. Thinking processes, unlike memory, develop slowly. In the lessons, your child will learn productive persistence, meaning he or she will encounter problems, at the right level and with the right level of scaffolding, that will build confidence.
Your child will be taught to
mastery.

To attain mastery, children are taught using Jerome Bruner’s C-P-A method (Concrete => Pictorial => Abstract) of first teaching with concrete materials, then progressing to pictures and finally to the abstract math language stage of learning. These are not discrete stages but overlapping stages. Once the child comprehends the abstract idea or situation, the concrete and pictures can be removed. In other words, the student can visualize the problem. He or she has a mental picture.
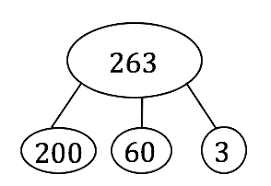
Mental math, the ability to manipulate and hold numbers in your head, is taught using special pictures called number bonds to build and break apart numbers. Mental math improves working memory and mental flexibility. It strengthens students’ number sense by reinforcing their understanding of place value, ability to find “friendly” numbers, computations skills, awareness that the same answer can be reached using different methods, and the capacity to hold information in their heads. Children get comfortable playing with numbers as they would playing with words. Number bonds are also used to help children master math facts and whole number operations.
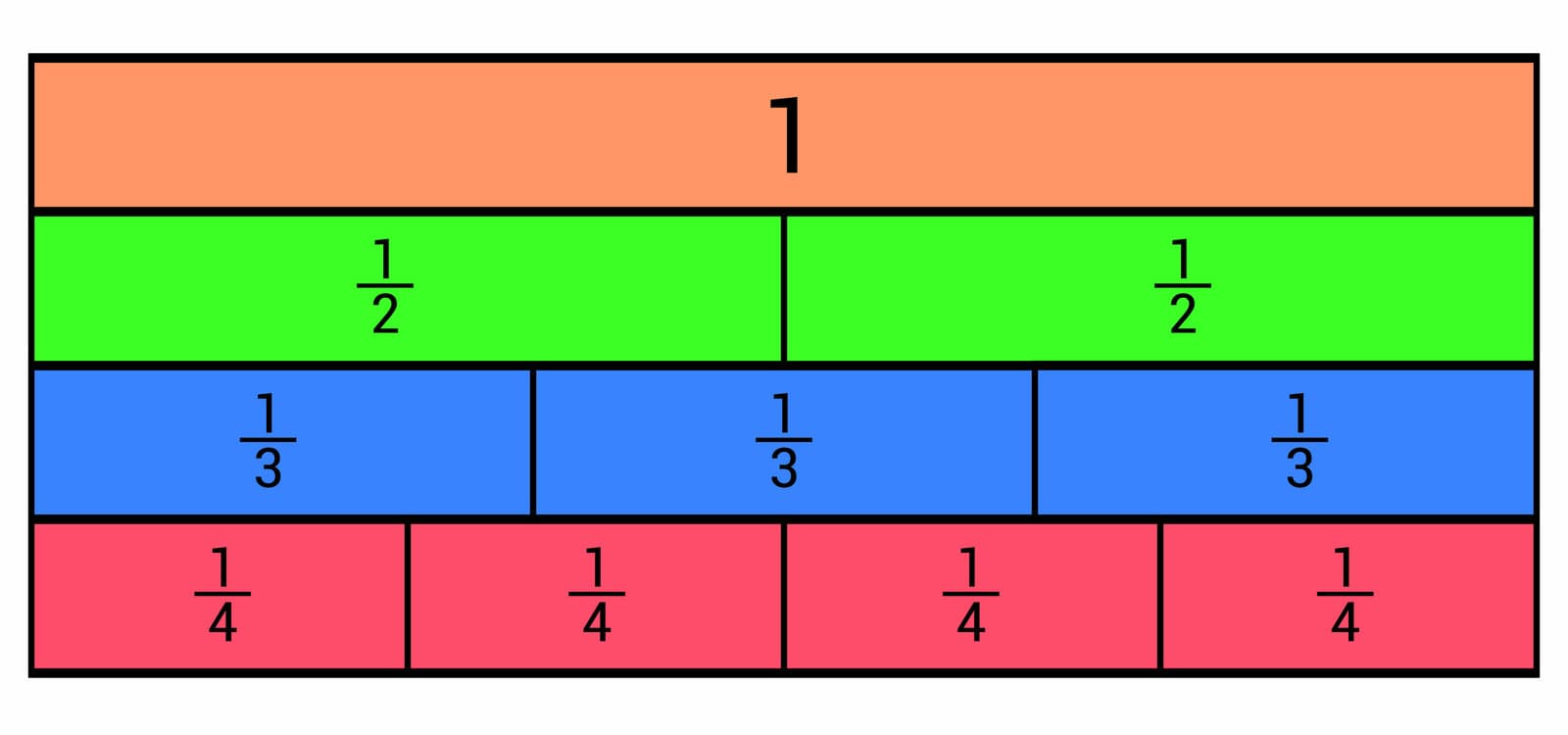
Children are also taught to draw special pictures called bar model pictures. Bar model pictures model a word problem in a way that makes the relationships and solution appear almost magically. Students learn that if they can “see’ the problem, they can solve the problem. Bar models are the essential visual tool for mastering word problems, especially algebraic, fraction and decimal problems.
Students who are struggling in math
benefit greatly from Singapore math lessons.
It’s common for a child to see me for math lessons because he or she is stuck in math, finding math too difficult, and math is not making sense because of a weak math foundation. Often the child has poor number sense, weak place value and hasn’t mastered math facts. If this is so, then, without intervention, the child will later struggle with math procedures such as column subtraction and long division. Without an understanding of how to add, subtract, multiply or divide, and mastery of math facts, the child will struggle to solve word problems involving whole number operations.
The sooner the child is identified as not having mastered math facts, the fewer the number of lessons he or she will need to catch up in math. Lack of math fact mastery is a gatekeeper to upper elementary math mastery. Mastery of math facts means understanding the operation, using strategies to solve, and attaining automatic fact recall.
Another place that students get stuck is with the concept of fractions. Utilizing the C-P-A (Concrete to Pictorial to Abstract) method, fractions are taught using different models, not just pizzas, so that you can take a fraction of anything including money, time, measurement as examples. With the Singapore approach, students gain a deep understanding of what fractions are and become confident in all operations and in applying them in many different word problems and situations.
Many students that see me are uncomfortable or fearful of word problems. The #1 visual tool that I can teach your child in math is how to use bar models to turn word problems into a picture that highlights the pattern and relationships so that your child can see the problem and solve it. As the foundational gaps are filled and your child is given the right tools to solve problems, he or she will become a confident, capable math student. I teach using a variety of Singapore math textbooks, workbooks, extra practice, word problem practice and specialized curricula called Visible Thinking and Math Works that are especially beneficial for visual learners.
Students who are naturally strong in
math benefit greatly from Singapore math lessons.

Strong math students benefit from a rigorous, cohesive Singapore program that introduces well-constructed word problems at an early age, as early as 1st grade as oral language and picture stories. In a Singapore program, strong math students are taught to be aware of and develop a set of good habits of mind and acquire a set of thinking skills and problem-solving heuristics. To improve their creative and critical thinking skills, students are also exposed to non-routine problems. When I teach students who are advanced in math or who are motivated to want more challenge, I can draw from many different Singapore sources including:
- Primary Mathematics Challenging Word Problems series,
- Primary Mathematics Intensive Practice,
- FAN-Math i-EXCEL Heuristic and Model Approach for Process Skills,
- and Brain Maths puzzles and brain teasers.
Primary Mathematics is the curriculum that originally put Singapore at the top of international math testing. With Singapore’s heuristic approach, your child will be systematically taught specific strategies such as working backwards, make a list, act it out, draw a diagram, simplify the problem, guess and test, and look for a pattern. Because your child will be taught to draw bar model pictures, he or she will encounter and solve word problems not typically encountered until later grades in US curriculum or in many cases, not at all. With these resources, bar models are taught in a step-by-step progression of complexity to master bar modeling in the shortest time possible.
Your child will be taught to international standards. In 2019 TIMSS international exams, 41% of Singapore students achieved the advanced benchmark while only 10% of the US students reached the advanced benchmark. 40% of the US students reached the high benchmark while 74% of Singapore’s students achieved the high benchmark.
Example of TIMSS Problem -Eighth Grade Item:
Question: The length of a rectangle is 6 cm, and its perimeter is 16 cm. What is the area of the rectangle in square centimeters?
Answer: 12 square cm
Measurement Question Correct Answer: Singapore 86%, Korea, 66%, Japan 65%, Canada 41%, France 36%, U.S. 22%.
The example above is a good example of a typical measurement word problem in Singapore curriculum. Students who are taught with the Singapore approach also have a distinct advantage when they get to Algebra because they’ve been exposed to algebraic thinking at an early age and they’re comfortable with the manipulation of numbers. Algebra involves the manipulation of abstract symbols (variables, coefficients, terms, etc.) and the application of mathematical properties. Students taught the Singapore way have learned how to do mental math by decomposing and recomposing numbers which later is formally introduced in middle school as mathematical properties.